Tato stránka obsahuje nevědecké vysvětlení některých pojmů určené pro každého, kdo se necítí být matematikem.
Karbicový graf
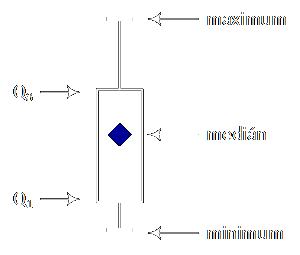Jde o grafické znázornění minima, maxima, mediánu, prvního a třetího kvartilu (Q1 a Q3). Hodnoty Q1 a Q3 tvoří pomyslnou krabičku, uvnitř ní je medián, maximum a minimum tvoří horní a dolní výčnělek krabičky.
Kdybychom seřadili data od nejmenší po největší a pak vybrali číslo přesně z prostředka (tedy dvou čtvrtin) tak získáme medián (tedy Q2). Pokud bychom vybrali hodnotu na hranici první čtvrtiny tak získáme Q1 a hodnota na hranici třetí čtvrtiny seřazených dat je Q3.
K čemu je testování hypotéz dobré?
Typickým příkladem pro testování hypotéz je sledování účinnosti nějaké metody nebo přípravku. Na několik vzorků nebo účastnících průzkumu se metoda nebo přípravek aplikuje a na několik nikoliv. Vznikne tak experimentální a kontrolní skupina. Sledovaná veličina se nejprve změří u všech subjektů. Pak se aplikuje přípravek nebo metoda u subjektů experimentální skupiny. Následně se sledovaná veličina opět změří u všech subjektů.
Například můžeme sledovat účinek nových rehabilitačních metod na 50-ti dobrovolnících. Řekněme, že budeme sledovat flexi kolenního kloubu v sagitální rovině. Změříme flexi před terapií. S 25-ti náhodně vybranými subjekty bude rehabilitováno klasicky a s 25-ti podle nových metod. Změříme flexi po rehabilitaci.
Většinou je na první pohled vidět, že v experimentální skupině došlo ke větší změně hodnot než u kontrolní skupiny. Nejvíce bývá změna patrná na hodnotě průměru. Chtěli bychom tuto změnu přisoudit pokusnému zásahu (např. novým metodám rehabilitace). Pozorovaný posun průměrné hodnoty ale může také být způsoben něčím jiným, například proměnlivostí měřené veličiny. V tom případě by pozorovaný posun nebyl statisticky významný a účinek pokusného zásahu by nemohl být prokazatelný. Proto se provádí statistikcé testy, které tuto možnost do určité míry vyloučí.
Hypotézy
Nejprve se formuluje nulová hypotéza, která tvrdí, že pokusný zásah byl neúčinný. Tuto hypotézu se snažíme vyvrátit. Pokud test ukáže neplatnost nulové hypotézy, pak se logicky přikloníme k alternativní. Ta by měla tvrdit opak, tedy, že pokusný zásah byl účinný.
Hladina statistické významnosti
Ani statistický test nám nemůže dát absolutní jistotu, abychom mohli tvrdit, že na 100% může za změnu pokusný zásah. Můžeme si ale předem nastavit toleranci vůči určitým chybám. Chyba „1.druhu“ je, že zamítneme nulovou hypotézu přesto, že platí. Hladina statistické významnosti říká s jakou pravděpodobností tato chyba nastane. Většinou si v sociologických a biologických oborech vystačíme s 5%.
Shapiro-Wilk test
Pomocí tohoto testu lze ověřit nakolik se rozložení daných dat blíží normálnímu rozdělení.
Na vodorovné ose jsou hodnoty naměřených dat. Na svislé ose jsou teoretické kvantily. Smyslem tohoto grafu je ukázat teoretickou pozici hodnot z daných dat. Pokud by rozdělení dat bylo normální, pak by se všechny body nacházeli na úhlopříčce.
